Origami lets us construct all constructions that are possible using ruler and compass (and more!)
Using origami, we can achieve segments, which lenghts are any rational number, using method shown in the video below. Proof is also in the video.
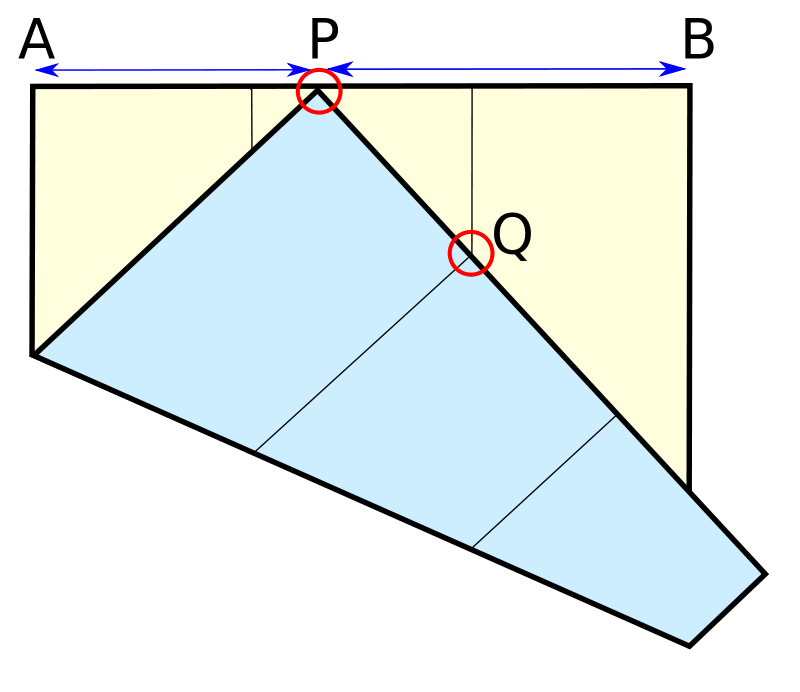
The famous classical problem of doubling the cube (that is, to cunstruct a segment of length equal to cube root of 2) can be solved using origami. This construction is due to Peter Messer. A square of paper is first creased into three equal strips. Then the bottom edge is positioned so the corner point P is on the top edge and the crease mark on the edge meets the other crease mark Q. The length PB will then be the cube root of 2 times the length of AP. The edge with the crease mark is considered a marked straightedge, impossible to construct using only ruler and compass. Using a marked straightedge in this way is called a neusis construction in geometry.
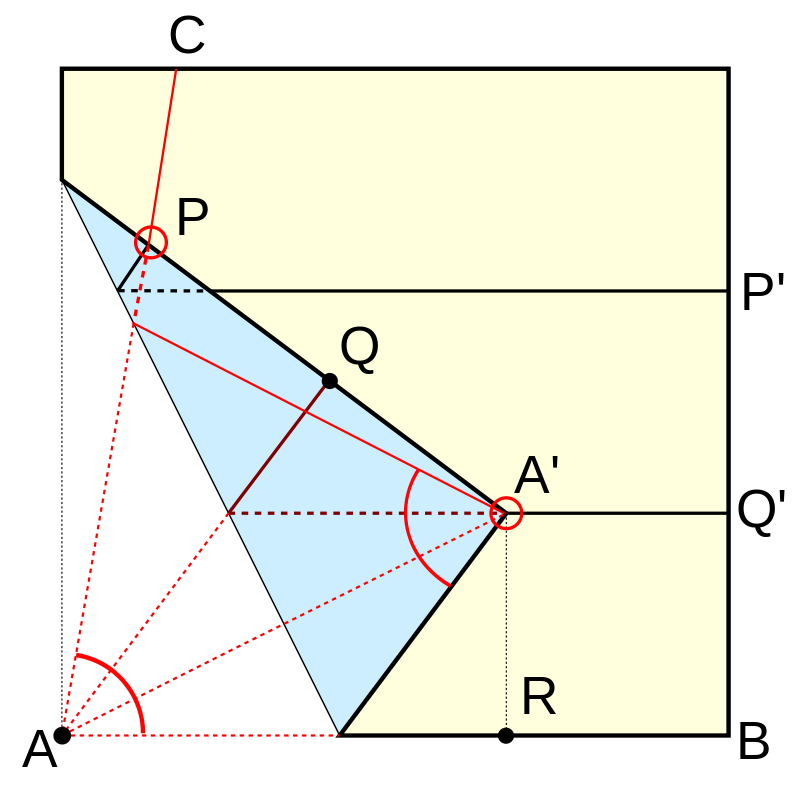
Another famous geometric problem is trisecting an angle. Similarily to doubling the cube, it is impossible using classical geometric tools, but possible having neusis construction allowed. This is why we can achieve it using origami. This construction is due to Hisashi Abe. The angle CAB is trisected by making folds PP' and QQ' parallel to the base and dividig sides in three equal parts. Then point P is folded over to lie on line AC and at the same time point A is made to lie on line QQ' at A'. The angle A'AB is one third of the original angle CAB. This is because PAQ, A'AQ and A'AR are three congruent triangles. Aligning two points on the two lines is another neusis construction as in the solution to doubling the cube.